As the nation drifts further into “fuck it” mode, the push to get big-time sports going continues to gain momentum. The NBA, NHL and MLB are all in the midst of devising ways to either resume or start their seasons. And not just before empty stadiums either. In fact, Ohio State University Athletic Director Gene Smith believes its famed Ohio Stadium (aka The Horseshoe) could accommodate at least 20,000 paying customers to watch the Buckeyes play college football this fall/winter:
Gene Smith says that if OSU could implement a crowd-size reduction plan along with CDC and local health distancing guidelines, OSU could accommodate maybe 20-22K fans for home games. Says they're very early in the process there.
— Jerod Smalley (@JerodNBC4) May 20, 2020
But is this actually possible? That is, could a gathering of 20,000 people indeed meet “local health distancing guidelines,” especially if, per the CDC, no two fans should be within 6 feet of each other.
To properly establish “COVID Capacity,” Matt Zaremsky, a math professor at the University at Albany suggests using the laws of uniform density. In the same way how knowing the density of a tablespoon of sugar can be used to determine the density of a bucket of sugar, “the stadium is large enough that it should have nearly uniform ‘people-per-square-foot density’ in both the normal and COVID scenarios,” he tells me.
In other words, finding the density of a small area of the crowd at full capacity can be extrapolated out to determine Ohio Stadium’s COVID Capacity.
To do so, Zaremsky suggests setting that small area to (obviously) a 6-foot radius. He estimates that at full capacity, which at The Horseshoe is 105,000, “there’d be something like 20 people within 6 feet of you in any direction.”
After that, the math becomes pretty simple — 105,000 divided by 20, equalling 5,250 people.
Even if there aren’t 20 people within your 6-foot bubble, Zaremsky adds that in order to get a “COVID capacity of 20,000 to 22,000,” you’d have to assume there are only five people within your 6-foot bubble in a packed Ohio Stadium, “which seems kind of ludicrous.”
Meanwhile, Sam Novario, a theoretical and computational nuclear physicist in Tennessee, “ran a quick little program” utilizing the size and depth of seating at The Horseshoe. Assuming its seats are the stadium average of 1.58 feet wide and its rows are the average of 2.17 feet deep, we can treat each seat as a rectangle.
Such rectangles allow Novario to execute what he calls “tessellation,” or creating “shapes that can be repeated like puzzle pieces to fill a plane.” (Apparently, we all learned this in high school.) It looks a little something like this:
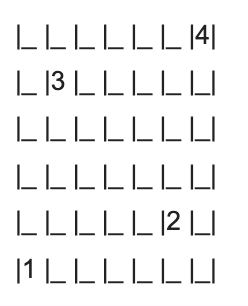
“The distance from 1 to 2 is 6.3 feet; the distance from 1 to 3 is 6.5 feet; and the distance from 2 to 3 is 6.4 feet,” Novario explains. This obviously forms a pattern where no matter if you’re person 1, 2, 3 or 4, you’ll always have at least 6 feet between you and anyone around you.
From there, the pattern continues until the stadium is full. “The pattern from 1 to 2 repeats itself after four applications, and the pattern from 1 to 3 repeats itself after five applications,” Novario says. “Therefore, each row has one seat filled for every 19 seats, and each row is offset five columns from the previous row.” (The pattern also minimizes people having to step over each other.)
Just look at all those beautiful, safe bubbles:
But the thing is, because there can only be one person every 19 seats, stadium capacity is limited to just 1/19th of its maximum. In pure math terms, then, Novario’s final tally is very similar to Zaremsky’s: 105,000 divided by 19, equalling 5,526 people.
Given that the pattern doesn’t account for places where people don’t sit, like stairs between sections, and less-dense areas like suites where seating won’t have to be restricted as much, Novario admits that his number might be conservative. Plus, he adds, “My calculation doesn’t take into account the height differences between rows.” Still, he says, “It’s hard to see how that would account for another 15,000 or so seats.”
All of which is to say a “packed” Horseshoe this college football season is probably far less than the wishful thinking of 22,000 (or even 20,000) screaming Buckeye fans.
Quinn Myers
Quinn Myers is a staff writer at MEL. He reports on internet culture, technology, health, masculinity and the communities that flourish within.
